کپیسیٹرز
(امیر سیف اللہ سیف)
Written by: Amir Saifullah Saif
کم قدر کے نان الیکٹرولائیٹک کپیسیٹرز کی قدریں کوڈ میں لکھی جاتی ہیں۔ مثال کے طور پر 882, 447, 332, 222, 123, 101 وغیرہ۔ اس کوڈ میں بائیں طرف کے دو ہندسے کپیسیٹر کی قدر کو اور دائیں طرف کا ہندسہ کپیسیٹر کی قدر میں صفروں کی تعداد کو ظاہر کرتا ہے۔اس طرح حاصل ہونے والی قدر پیکو فیراڈز (pF) میں حاصل ہوتی ہے۔ مثلاً اگر کپیسیٹر پر لکھا ہوا کوڈ 101 ہو تو اس کی قدر 100pF ہوگی۔ (بائیں طرف کے دو ہندسے 10 ہیں جبکہ دائیں طرف کا ہندسہ 1 ہے اس طرح ہم 10 کے ساتھ ایک صفر کا اضافہ کرکے اسے 100 بنا لیں گے)۔ اسی طرح 123 کوڈ کا مطلب 12000pF ہوگا۔ الیکٹرونکس ڈائجسٹ میں کپیسیٹرز کی قدریں لکھتے وقت فیراڈ کو ظاہر کرنے والا حرف F نہیں لکھا جاتا کیونکہ کپیسیٹر کی قدر فیراڈز ہی میں ہوتی ہے۔
پیکو فیراڈز میں حاصل ہونے والی قدر اگربہت زیادہ ہو تو اسے 1000 پر تقسیم کر کے نینو فیراڈز (nF) میں اورنینو فیراڈز کو 1000 پر تقسیم کرکے مائیکرو فیراڈز (µF) میں تبدیل کیا جا سکتا ہے۔ ذیل میں دی گئی مثالوں سے اس کی وضاحت ہو جائے گی۔
| کوڈ | pF قدر | nF قدر | µF قدر | کوڈ | pF قدر | nF قدر | µF قدر |
|---|---|---|---|---|---|---|---|
| 102 | 1,000 | 1n0 | 0µ001 | 273 | 27,000 | 27n | 0µ027 |
| 122 | 1,200 | 1n2 | 0µ0012 | 303 | 30,000 | 30n | 0µ030 |
| 152 | 1,500 | 1n5 | 0µ0015 | 333 | 33,000 | 33n | 0µ033 |
| 162 | 1,600 | 1n6 | 0µ0016 | 393 | 39,000 | 39n | 0µ039 |
| 182 | 1,800 | 1n8 | 0µ0018 | 403 | 40,000 | 40n | 0µ04 |
| 202 | 2,000 | 2n0 | 0µ002 | 453 | 45,000 | 45n | 0µ045 |
| 222 | 2,200 | 2n2 | 0µ0022 | 473 | 47,000 | 47n | 0µ047 |
| 252 | 2,500 | 2n5 | 0µ0025 | 503 | 50,000 | 50n | 0µ05 |
| 272 | 2,700 | 2n7 | 0µ0027 | 563 | 56,000 | 56n | 0µ056 |
| 332 | 3,300 | 3n3 | 0µ0033 | 603 | 60,000 | 60n | 0µ06 |
| 392 | 3,900 | 3n9 | 0µ0039 | 683 | 68,000 | 68n | 0µ068 |
| 402 | 4,000 | 4n0 | 0µ004 | 753 | 75,000 | 75n | 0µ075 |
| 472 | 4,700 | 4n7 | 0µ0047 | 823 | 82,000 | 82n | 0µ082 |
| 502 | 5,000 | 5n0 | 0µ005 | 104 | 100,000 | 100n | 0µ1 |
| 522 | 5,200 | 5n2 | 0µ0052 | 124 | 120,000 | 120n | 0µ12 |
| 562 | 5,600 | 5n6 | 0µ0056 | 154 | 150,000 | 150n | 0µ15 |
| 602 | 6,000 | 6n0 | 0µ006 | 184 | 180,000 | 180n | 0µ18 |
| 652 | 6,500 | 6n5 | 0µ0065 | 204 | 200,000 | 200n | 0µ20 |
| 682 | 6,800 | 6n8 | 0µ0068 | 224 | 220,000 | 220n | 0µ22 |
| 702 | 7,000 | 7n0 | 0µ007 | 274 | 270,000 | 270n | 0µ27 |
| 752 | 7,500 | 7n5 | 0µ0075 | 304 | 300,000 | 300n | 0µ3 |
| 802 | 8,000 | 8n0 | 0µ008 | 334 | 330,000 | 330n | 0µ33 |
| 822 | 8,200 | 8n2 | 0µ0082 | 394 | 390,000 | 390n | 0µ39 |
| 852 | 8,500 | 8n5 | 0µ0085 | 404 | 400,000 | 400n | 0µ4 |
| 902 | 9,000 | 9n0 | 0µ009 | 474 | 470,000 | 470n | 0µ47 |
| 952 | 9,500 | 9n5 | 0µ0095 | 504 | 500,000 | 500n | 0µ5 |
| 103 | 10,000 | 10n | 0µ01 | 564 | 560,000 | 560n | 0µ56 |
| 123 | 12,000 | 12n | 0µ012 | 684 | 680,000 | 680n | 0µ68 |
| 153 | 15,000 | 15n | 0µ015 | 754 | 750,000 | 750n | 0µ75 |
| 163 | 16,000 | 16n | 0µ016 | 824 | 820,000 | 820n | 0µ82 |
| 193 | 18,000 | 18n | 0µ018 | 904 | 900,000 | 900n | 0µ9 |
| 203 | 20,000 | 20n | 0µ02 | 954 | 950,000 | 950n | 0µ95 |
| 223 | 22,000 | 22n | 0µ022 | 105 | 1,000,000 | 1000n | 1µ0 |
آپ دیکھ رہے ہیں کہ اس مثا ل میں m0.022 کو 022m0 اور دوسری قدروں کوبھی اسی طرح لکھا گیا ہے۔ یہاں بھی اعشاریہ کے نشان کی جگہ قدر ظاہر کرنے والا حرف لکھا گیا ہے تاکہ پڑھنے میں آسانی ہو۔ دو یا زائد کپیسیٹرمتوازی (Paralell) جوڑنے سے ان کی کپیسی ٹینس جمع ہو جاتی ہے مثال کے طور پر
متوازی (Paralell) جڑے ہوئے کپیسیٹرز کی قدر معلوم کرنے کا فارمولا .... +C1+C2+C3 ہے۔ دو یا زائد کپیسیٹرز سلسلے وار (Series) جوڑنے سے ان کی مجموعی کپیسی ٹینس‘ کم سے کم قدر کے کپیسیٹر سے بھی کم ہو جاتی ہے مثال کے طور پر:
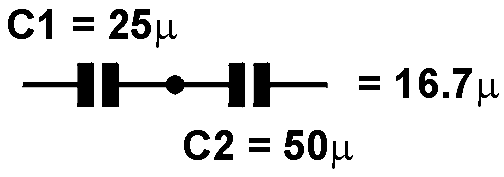
سلسلے وار جڑے ہوئے دو کپیسیٹرز کی قدر معلوم کرنے کا فارمولا مندرجہ ذیل ہے :
دو سے زائد سلسلے وار جڑے ہوئے کپیسیٹرز کی قدر معلوم کرنے کا فارمولا مندرجہ ذیل ہے :
اگر ان کی وضاحت نہ کی گئی ہوتو تمام کپیسیٹر عام طور پر 60V کے ہوں گے۔ عام اصول کے مطابق کپیسیٹر کے ورکنگ وولٹیج‘ سرکٹ میں موجود وولٹیج کی نسبت کم از کم دگنے ضرور ہوں۔
کپیسیٹر کی قدر سے اس کا کوڈ یا اس کے کوڈ کی مدد سے اس کی قدر معلوم کرنے کے لیے کپیسیٹر کوڈ / قدر کیلکولیٹر استعمال کیا جا سکتا ہے۔
